1's and 2's Complement
1's Complement: Reciprocal of 1s to 0s and 0s to 1s is its 1's complement. For eg, 1's Complement of (1011)2 is (0100)2
2's Complement: Adding 1 to the 1's complement of a given binary number is its 2's complement.
For eg, if (1010)2 is a given number then, its
1's complement is (0101)2 and 2's complement is (0101)2 +(1)2 = (0110)2
Very important
Subtraction using 1's and 2's Complement
Rules to remember [ let us consider, question be X-Y] | |
| Using 1's Complement | Using 2's Complement |
| Calculate 1's complement of ‘Y’ | Calculate 2's complement of ‘Y’ |
| Add result of step 1 with ‘X’ | Add result of step 1 with ‘X’ |
| If there is extra bit, remove that extra bit and add on its remaining bit. | If there is extra bit, remove that extra bit. |
| If there is no extra bit, find 1's Complement of result in step 2 and add (-)ve sign. | If there is no extra bit, find 2's Complement of result in step 2 and add (-)ve sign. |
Example ( Sure question for Board exam)
Q) Subtract (1000)2 from (111)2 using 1's and 2's complement.
Ans. Given question is (111)2 - (1000)2
A) Using 1's Complement,
First calculating 1's complement of (1000)2 is (0111)2
Adding (0111)2 with (111)2 we get
(0111)2 + (0111)2 = (1110)2
Since, there is no extra bit i.e. 4 digits added with 4 digits and gives 4 digits result
Calculating 1's complement of (1110)2 we get (0001)2 and putting (-)ve sign
Hence, result is -(0001)2
B) Using 2's Complement,
First calculating 2's complement of (1000)2 is (0111)2 + (1)2 = (1000)2
Adding (1000)2 with (111)2 we get
(1000)2 + (0111)2 = (1111)2
Since, there is no extra bit i.e. 4 digits added with 4 digits and gives 4 digits result
Calculating 2's complement of (1111)2 we get (0000)2 + (1)2 = (0001)2 and putting (-)ve sign
Hence, result is -(0001)2
Q) Subtract (11001)2 from (11101)2 using 1's and 2's complement.
Ans. Given question is (11101)2 - (11001)2
A) Using 1's Complement,
First calculating 1's complement of (11001)2 is (00110)2
Adding (00110)2 with (11101)2 we get
(00110)2 + (11101)2 = (100011)2
Since, there is extra bit i.e. 5 digits added with 5 digits and gives 6 digits result
Removing that extra bit and adding on it
(00011)2 + (1)2 = (00100)2
Hence, result is (00100)2
B) Using 2's Complement,
First calculating 2's complement of (11001)2 is (00110)2 + (1)2 = (00111)2
Adding (00111)2 with (11101)2 we get
(00111)2 + (11101)2 = (100100)2
Since, there is extra bit i.e. 5 digits added with 5 digits and gives 6 digits result
Removing that extra bit, we get (00100)2
Hence, result is (00100)2
1s and 2s complement subtraction
1's and 2's Complement
1's Complement can be obtained by simply altering 1s to 0s and 0s to 1s. For eg, 1's Complement of (1001) is (0110). Similarly 2's Complement can be obtained by Adding 1 to the 1's complement of a given binary number. For eg, if (1001) is a given number then, its 1's complement is (0110) and 2's complement is (0110) +(1) = (0111)
Rules in 1s and 2s complement subtraction
Rule using 1s Complement
Step 1: Given numbers must be in the form X-Y with same digits. Extra 0 can be added at the beginning to make same digits.
Step 2: Calculate 1's complement of ‘Y’
Step 3: Add result of step 2 with ‘X’
Step 4: If there is extra bit, remove that extra bit and add on its remaining bit.
If there is no extra bit, find 1's Complement of result in step 3 and add (-)ve sign.
Rule using 2s Complement
Step 1: Given numbers must be in the form X-Y with same digits. Extra 0 can be added at the beginning to make same digits.
Step 2: Calculate 2’s complement of ‘Y’
Step 3: Add result of step 2 with ‘X’
Step 4: If there is extra bit, remove that and remaining bit will be the answer.
If there is no extra bit, find 2’s Complement of result in step 3 and add (-)ve sign.
Q1) Subtract (1010) from (1111) using 1's and 2's complement.
Ans. Given question is (1111) - (1010)
A) Using 1's Complement,
First calculating 1's complement of (1010) is (0101)
Adding (0101) with (1111) we get
(0101) + (1111) = (10100)
Since, there is extra bit i.e. 4 digits added with 4 digits and gives 5 digits result
Removing that extra bit and adding on it
(0100) + (1) = (0101)
Hence, result is (0101)
B) Using 2's Complement,
First calculating 2's complement of (1010) is (0101) + (1) = (0110)
Adding (0111) with (1101) we get
(0110) + (1111) = (10101)
Since, there is extra bit i.e. 4 digits added with 4 digits and gives 5 digits result
Removing that extra bit, we get (0101)
Hence, result is (0101)
Q2) Subtract (100) from (11) using 1's and 2's complement.
Ans. Given question is (11) - (100), making same digits we have (011) - (100)
A) Using 1's Complement,
First calculating 1's complement of (100) is (011)
Adding (011) with (011) we get
(011) + (011) = (110)
Since, there is no extra bit i.e. 3 digits added with 3 digits and gives 3 digits result
Calculating 1's complement of (110) we get (001) and putting (-)ve sign
Hence, result is -(001)
B) Using 2's Complement,
First calculating 2's complement of (100) is (011) + (1) = (100)
Adding (100) with (011) we get
(100) + (011) = (111)
Since, there is no extra bit i.e. 3 digits added with 3 digits and gives 3 digits result
Calculating 2's complement of (111) we get (000) + (1) = (0001) and putting (-)ve sign
Hence, result is -(001)
Q3) Subtract (1001) from (1101) using 1's and 2's complement.
Ans. Given question is (1101) - (1001)
A) Using 1's Complement,
First calculating 1's complement of (1001) is (0110)
Adding (0110) with (1101) we get
(0110) + (1101) = (10011)
Since, there is extra bit i.e. 4 digits added with 4 digits and gives 5 digits result
Removing that extra bit and adding on it
(0011) + (1) = (0100)
Hence, result is (0100)
B) Using 2's Complement,
First calculating 2's complement of (1001) is (0110) + (1) = (0111)
Adding (0111) with (1101) we get
(0111) + (1101) = (10100)
Since, there is extra bit i.e. 4 digits added with 4 digits and gives 5 digits result
Removing that extra bit, we get (0100)
Hence, result is (0100)
Q4) Perform (111100) - (1011) using 1's and 2's complement.
Ans.Given question is (111100) - (1011), making same digits we have (111100) - (001011)
A) Using 1's Complement,
First calculating 1's complement of (001011) is (110100)
Adding (110100) with (111100) we get
(110100) + (111100) = (1110000)
Since, there is extra bit i.e. 6 digits added with 6 digits and gives 7 digits result
Removing that extra bit and adding on it
(110000) + (1) = (110001)
Hence, result is (110001)
B) Using 2's Complement,
First calculating 2's complement of (001011) is (110100) + (1) = (110101)
Adding (110101) with (111100) we get
(110101) + (111100) = (1110001)
Since, there is extra bit i.e. 6 digits added with 6 digits and gives 7 digits result
Removing that extra bit, we get (110001)
Hence, result is (110001)
Q5) Perform (1010) - (101111) using 1's and 2's complement.
Ans. Given question is (1010) - (101111), making same digits we have (001010) - (101111)
A) Using 1's Complement,
First calculating 1's complement of (101111) is (010000)
Adding (010000) with (001010) we get
(010000) + (001010) = (011010)
Since, there is no extra bit i.e. 6 digits added with 6 digits and gives 6 digits result
Calculating 1's complement of (011010) we get (100101) and putting (-)ve sign
Hence, result is -(100101)
B) Using 2's Complement,
First calculating 2's complement of (101111) is (010000) + (1) = (010001)
Adding (010001) with (001010) we get
(010001) + (001010) = (011011)
Since, there is no extra bit i.e. 6 digits added with 6 digits and gives 6 digits result
Calculating 2’s complement of (011011) we get (100100) + (1) = (100101) and putting (-)ve sign
Hence, result is -(100101)
Introduction: Boolean Logic
Boolean Algebra is algebra of logic, which deals with the study of binary variables and logical operation. As every data are represented in terms binary values, we need to manipulate those values by using some certain rules and expression which we can do through Boolean algebra. It is most common and basic method to analysis and design logic circuit. It was introduced by an English mathematician George Boole. In Boolean algebra the variables can have only one of the two possible value 0 and1 (False or True). Every modern digital computers understand either this two values.
Boolean algebra: It is algebra of logic which could accept either of the possible two values 0 and 1 and generate a result through logical relationship and operation.
Boolean variable: Those entities which has either or 0 and 1 and denote some specific operation ore known as boolean variable. Simply, it is an entity in Boolean algebra which has only either of the two possible values. This variable are denoted by A, B, P, Q, X, Y, Z….
Boolean function (logic functions): Boolean function is an expression formed by binary variables, binary operators such as AND, OR, NOT, parentheses, and equal sign for a given set of value this boolean function gives the 0 or 1 as a result.
let us consider,
F = XYZ’+XY
Where, F is a boolean function
X, Y, Z are a boolean variable.
X, Y, Z, Z’ are also literals.
Truth Table: A table which represents the input-output relationship between of the binary variables for each logical gate called truth table. It shows the relationship between input and output in tabular form. Thus, truth table is table representing the results the logical operation of the logical operation on all possible combination of logical values.
Boolean Operator and Operands
Operators are the symbols that define the specific operation. These are three basic operators used in Boolean Algebra, ie. AND, OR, NOT. Every other operations can be expressed in terms of this basic operation. For examples, NOR operator is the combination of NOT and OR operators. The three basic operators are:
a. AND Operators: AND operator is represented by “.” So, A AND B is represented by (A.B) . The result of the AND operation is exactly same as simple arithmetic multiplication. That means result will be high (1) only when both the inputs are high. Note: A AND B can also represented bu AˆB or AnB. Truth table of AND operation is given below
| A | B | Y = A.B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
b. OR Operator: OR operator is represented by “+” So, A OR B is represented by (A+B) . The result of the OR operation is exactly same as simple arithmetic addition. That means result will be low (0) if and only both the inputs are low. Note: A OR B can also represented bu AvB or AuB. Truth table of AND operation is given below
| A | B | Y = A+B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
c. NOT Operator: NOT operator is represented by “-” or “ ’ ” So, NOT operation of an operands A is represented as A’ . NOT operation performs negation. That means it will give high output (1) for low input (0) and vice-versa. Truth table of NOT operation is given below
| A | A' |
| 0 | 1 |
| 1 | 0 |
Logic Gate
A logic Gate is an electronic circuit that operates on one or more inputs to produce an output. Logic Gate are used for binary operations which are very fundamental components for modern digital computer. Logic gates are embedded unit an Integrated Circuit (IC). Each gate has its specific function and graphical symbol. In digital computer there are three basic logic gates.
Every digital computer has digital circuits (IC, LSI) to perform binary operations. These digital circuits are made up of several logic gates and their combination. Thus, logic gates is the basic component of digital computer that operates on one or more input signals to produce an output signal. Each gates has its own specific function, algebraic expression, gate symbol and truth table. In a digital computer AND, OR, NOT are the three fundamental basic gates whereas, NAND, NOR, X-OR, X-NOR are the derived gates from the basic gates. All the logic gates are explained:
AND gate
It is an electronic circuit, which produce high logic (1) output when both the input logic are high (1) and produce low logic(0) when any one of the input logic is low (0). The output produce by this basic gate is the product of its input logic.
Algebraic expression
F=A.B where, A and B are inputs, F is an output and “.” Denotes AND operation
Gate symbol;
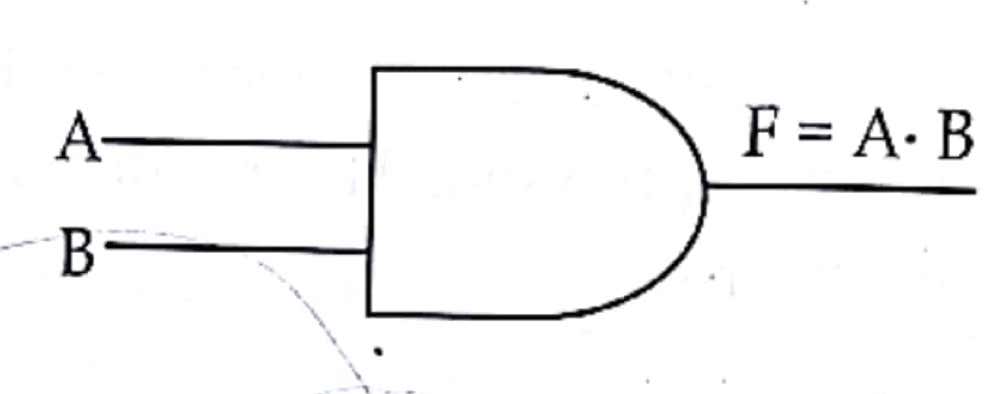
Truth Table:
| A | B | F=A.B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Venn diagram:
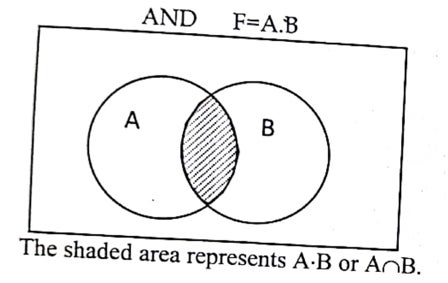
OR gate
It is an electronic circuit, which produce high logic (1) output when any one of the input logic are high (1) and produce low logic(0) when both the input logic is low (0). The output produce by this basic gate is the sum of its input logic.
Algebraic expression:
F=A+B where, A and B are inputs, F is an output and “+” Denotes OR operation
Gate symbol:

Truth Table:
| A | B | F=A+B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Venn diagram:
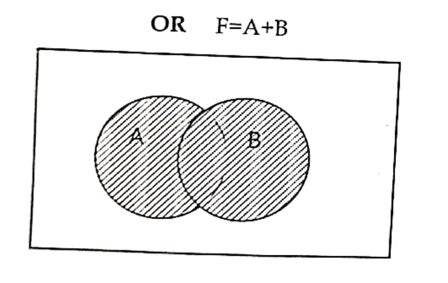
NOT gate
It is an electronic circuit, which produce high logic (1) output when the input logic is low (0) and produce low logic(0) when the input logic is high (1). The output produce by this basic gate is the reciprocal of its input logic.
Algebraic expression:
F=A’ where, A is inputs, F is an output
Gate symbol:
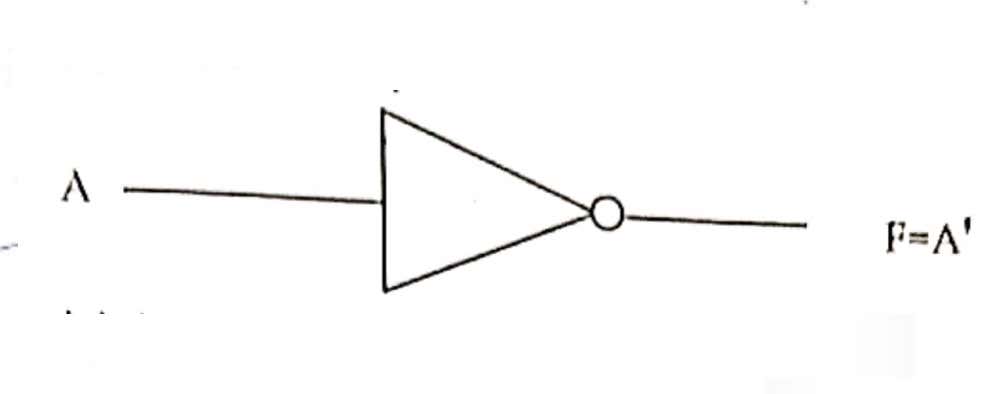
Truth Table:
| A | F=A’ |
| 0 | 1 |
| 1 | 0 |
Venn diagram:
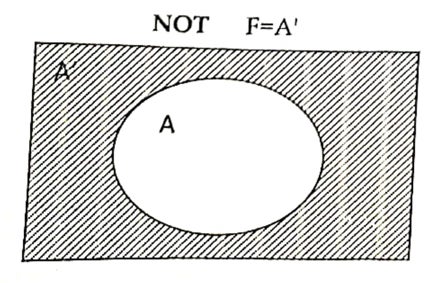
NAND gate
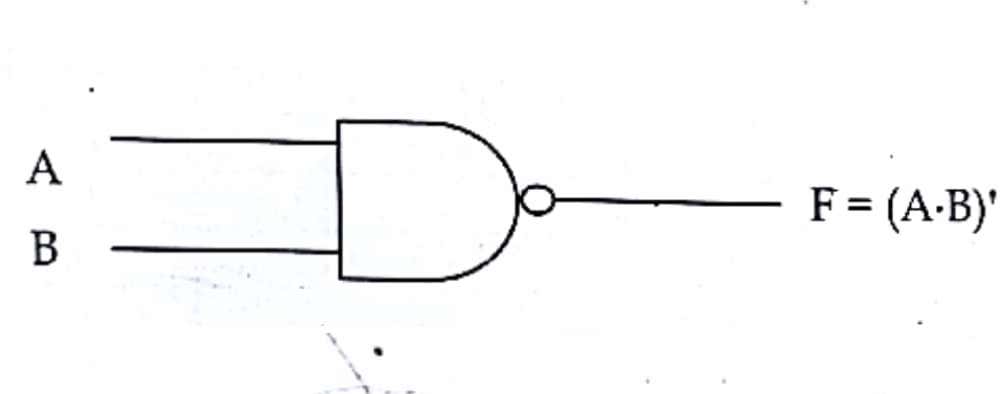
It is the combination of NOT and AND gate, which produce high logic (1) output when any one of the input logic is low (0) and produce low logic(0) when both the input logic is high (1). The output produce by this basic gate is the reciprocal or complement of AND gate. It is also known as derived gate.
Algebraic expression:
F=(A.B)’ where, A and B are inputs, F is an output.
Gate symbol:
Truth Table:
| A | B | A.B | F=(A.B)’ |
| 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Venn diagram:
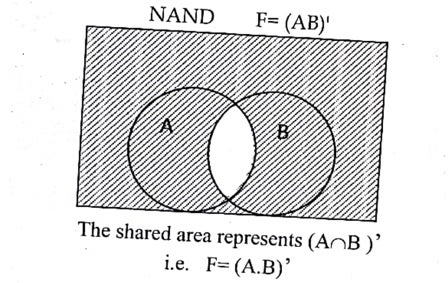
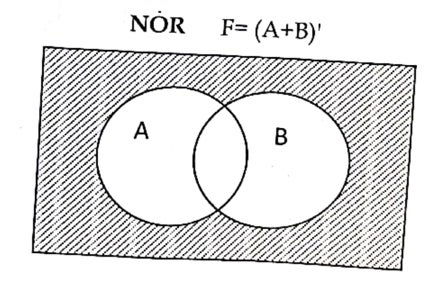
NOR gate
It is the combination of NOT and OR gate, which produce high logic (1) output when both the input logic is low (0) and produce low logic(0) when any one of the input logic is high (1). The output produce by this basic gate is the reciprocal or complement of OR gate. It is also known as derived gate.
Algebraic expression:
F=(A+B)’ where, A and B are inputs, F is an output.
Gate symbol:
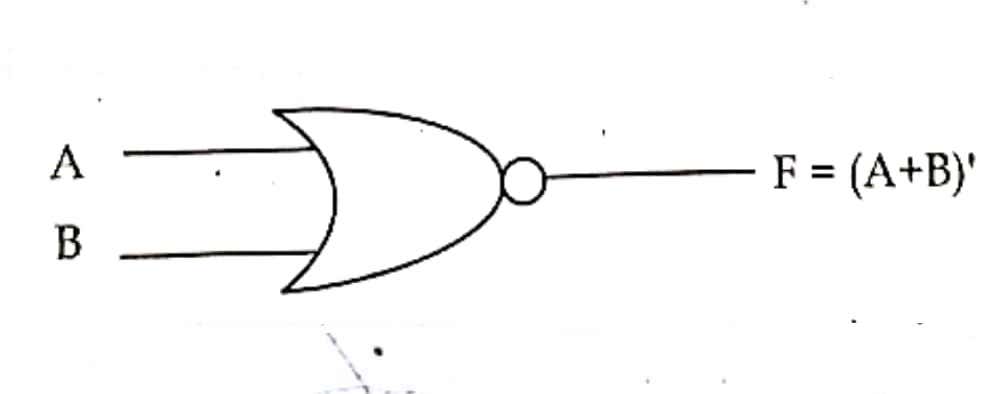
Truth Table:
| A | B | F=A+B | F=(A+B)’ |
| 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 |
Venn diagram:
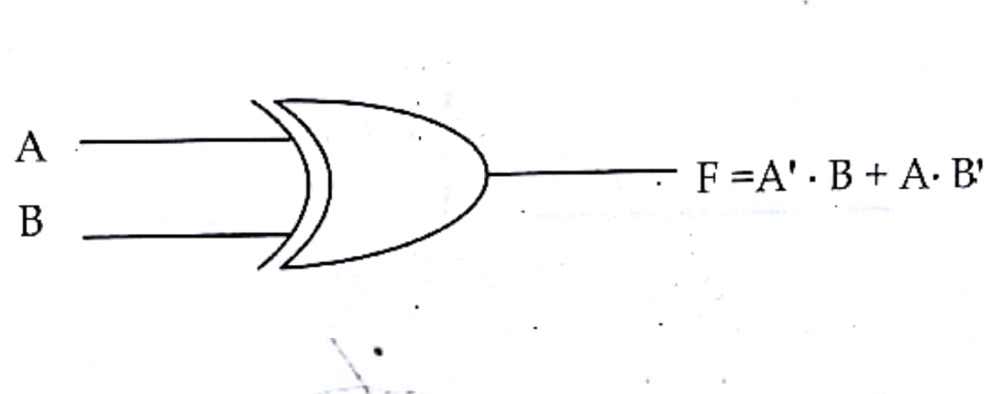
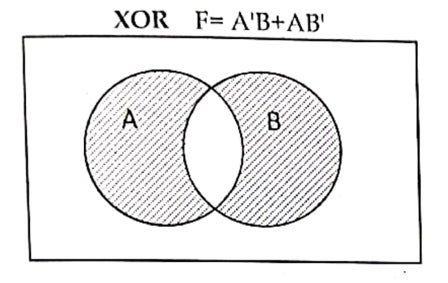
X-OR gate
It is derived gate, which produce low logic (0) output when both the input logic are either high (1) or low (0) otherwise it will produce high logic(1).
Algebraic expression:
F=A’.B+A.B’ where, A and B are inputs, F is an output.
Gate symbol:
Truth table:
| A | B | A’ | B’ | A’.B | A.B’ | A’.B+A.B’ |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 |
Venn diagram:
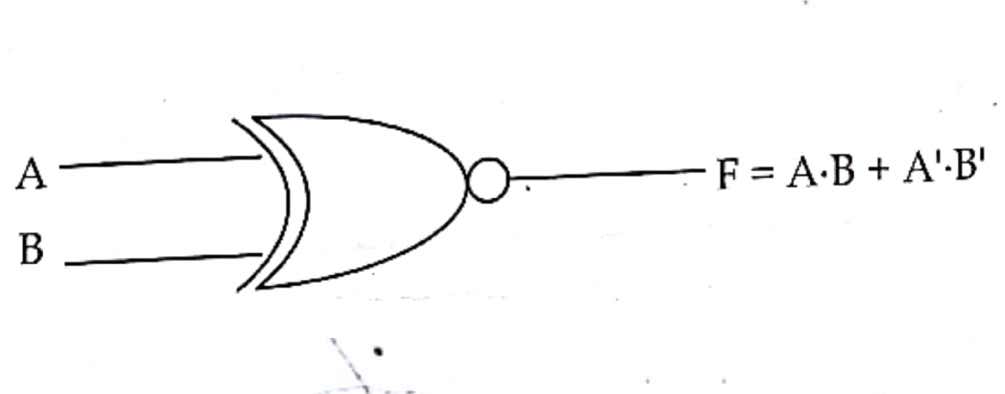
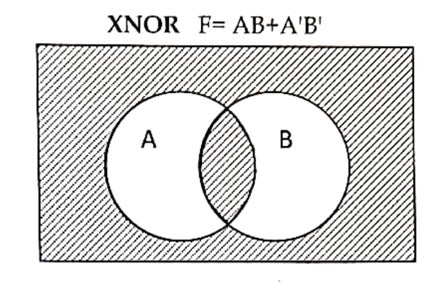
X-NOR gate
It is derived gate, which produce high logic (1) output when both the input logic are either high (1) or low (0) otherwise it will produce low logic(0).
Algebraic expression:
F=A.B+A’.B’ where, A and B are inputs, F is an output.
Gate symbol:
Truth table:
| A | B | A’ | B’ | A.B | A’.B’ | A’.B+A.B’ |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 1 |
Venn diagram:
a. AND gate: AND Gate is an electronic Circuit which produce high output (1) only when both the inputs are high. The output is same as the result of basic arithmetic multiplication. This gate may have more than two inputs and produce a single output. Graphically AND gate is represented as
AND gate is denoted by “ . ” So, output is expressed algebraically as, Y = A
Truth table for AND gate is
| A | B | Y = A.B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
b. OR Gate: OR Gate is an electronic circuit which produce low output (0), when all the inputs are low (0) and produce high (1) output for every possible combination of 0 and 1. The output is same as basic binary addition. The gate may have two or more than two inputs and produce single result.
Graphically OR gate is represented as
Algebraically output of OR Gate is represented as: Y = A+B
Truth table of OR Gate is
| A | B | Y = A+B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
c. NOT Gate: NOT Gate is another fundamental gate whose result is complement of its input. It is also called inverter. It produces low-0 logic for high-1 input and vice-versa. This Gate has single input and single output. Graphically NOT gate is represented as:
Algebraically output of NOT Gate is represented as: Y = A’ for input A
Truth table of NOT gate is:
| A | A' |
| 0 | 1 |
| 1 | 0 |
d. NAND Gate: NAND gate is a derived gate, derived from NOT and AND gate. This gate reciprocal the output obtain from the AND gate. That means it will produce low-0 output when both the inputs are high-1 and produce high-1 output when any one of the input is low-0. These gate also may have two or more than two and a single output.
Graphically NAND gate is represented as:
Algebraically output of NAND Gate is represented as: Y = (A.B)’
Truth table of NAND Gate is:
| A | B | A.B | y=(A.B)' |
| 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
e. NOR gate: NOR gate is a derived gate derived from the combination of OR gate and NOT gate. This gate reciprocal the output obtain from the OR gate. That means NOR gate will produce high-1 logic when both the inputs are low-0 and produce low output-0 in all possible combination of 0 and 1. These gate also may have two or more than two input at a single output.
Graphically NOR gate is represented as
Algebraically output of NOR gate is represented as: Y: (A+B)’
Truth Table of NOR gate is
| A | B | A+B | Y = (A+B)' |
| 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 |
f. Exclusive OR (X-OR): It is the type of digital electronic circuit will generates low-0 output when both the inputs are either low-0 or high-1. It will give high-1 output only when one of the given input is high. These gate also may have two or more the two input.
Graphically X-OR gate is represented as
Algebraically output of X-OR gate is represented as: Y: A’.B + A.B’
Truth Table of X-OR gate is
| A | B | A' | B' | A'.B | A.B' | A'.B+A.B' |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 |
g. Exclusive NOR (X-NOR): It is the type of digital electronic circuit will generates high-1 output when both the inputs are either low-0 or high-1. It will give low-0 output only when one of the given input is high-1. These gate also may have two or more the two input.
Graphically X-NOR gate is represented as
Algebraically output of X-NOR gate is represented as: Y: A.B + A’.B’
Truth Table of X-NOR gate is
| A | B | A' | B' | A.B | A'.B' | A.B+A'.B' |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 1 |
De-Morgan's Theorem
First Theorem: The De-Morgan's first theorem states that, “The complement of a sum equals to the product of its complement.”
It is represented as: (A+B)' = A'.B''
Graphical symbol
Proof:
| A | B | (A+B) | (A+B)' | A' | B' | A'.B' |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
Second Theorem: The De-Morgan's second theorem states that, “The complement of a product equals to the sum of its complement.”
It is represented as: (A.B)' = A'+B''
Graphical symbol
Proof:
| A | B | (A.B) | (A.B)' | A' | B' | A'+B' |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |